「调和数」是毕达哥拉斯学派[1]从琴弦长度的研究上发现的一种数量关系。他们发现，一根拉紧的琴弦（1倍长的琴弦）如果弹出某个音调，比如说是do，那么取其1/2弦长，弹出的音调就是高八度的do，取其 2/3 弦长，就会弹出高五度的so。

弦长少一半，振动频率增加一倍，同理，弦长为原来的2/3，那么频率为原来的3/2.

147*2=294

294/2*3=441

毕达哥拉斯定理就是勾股定理。

爱因斯坦12岁仅用相似三角形的性质证明了勾股定理

利用五度音、八度音，毕达哥拉斯还提出了五度相生律，对每个音的音高进行定量化。举个简单的例子，我们唱歌中的do(1)、re(2)、mi(3)、fa(4)、sol(5)、la(6)、si(7)，每个音是如何确定出来的？

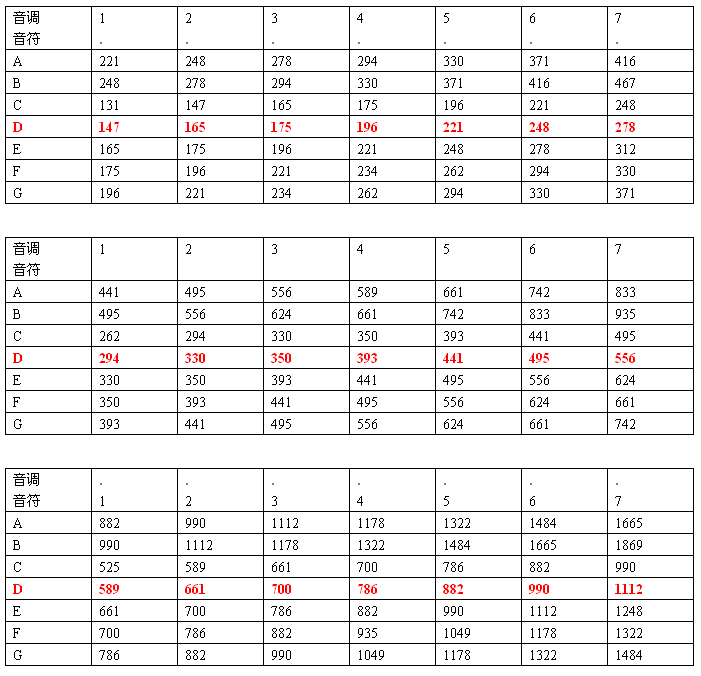
由琴弦定律可知，在张力一定的情况下，弦长与发音频率成反比关系。人们把频率相差一倍的音称为纯八度音，例如从do(1)到“高音的do(1)”，从re(2)到“高音的re(2)”，以此类推，它们相差纯八度，频率相差一倍。五度音就是频率比为3:2的音，例如从do(1)到sol(5)，从re(2)到la(6)等等就是五度音。

先设定一个标准音，比如do(1)，若将弦长缩短为原来的2/3，音升五度可得到sol(5)；同理，re(2)升五度可得到la(6)，mi(3)升五度可得到si(7)，还缺re(2),mi(3),fa(4)。为了得到re(2)先将sol(5)升五度至"高音的re(2)"，再利用弦长增加一倍频率降低为一半，降八度调整得到re(2)；通过类似的先升再降的办法就可以得到mi(3)和fa(4)。利用该方法，可得到任一音高。当然，类似的方法也可以向降音的方向行进，获得全音域的音。

在音乐中音律就是调，我们常说定个基调，然后再开唱和上面的做法是一致的。我们常听说的C调，D调，E调等，其实就是在do(1)、re(2)、mi(3)、fa(4)、sol(5)、la(6)、si(7)选谁为do(1)的意思，如果选do(1)就是C调，选re(2)就是D调，选mi(3)就是E调，在一个循环中共7个调，分别为CDEFGAB调。由此可见琴弦定律在音乐中的作用和意义不可小觑。

362573 EADGBE吉他六弦

五度相生律的数学计算

十二平均律算得上是音乐与数学中的一个巧合

金字塔密码432：有个男人测量了金字塔，并暗示了他发现的秘密