微积分教学(一):割圆法求圆面积
绘制多边形来微分圆。根据任意凸多边形的外角和都为360°。画固定周长(1000)的多边形。可以看到,边数越多,越趋近于圆。 也就是说如果边长越小,那么地平线越平坦。越没有弧度。 半径(楞到圆心)为10
定积分:牛顿-莱布尼茨公式
已知函数面积的导数就是原函数
如何一刀切出四分之一的蛋糕
牛顿迭代法来计算圆的切割角度 如何一刀切出四分之一的蛋糕
割圆法求圆周率和圆面积(附带进度条)
割圆法求圆面积,当半径为1000时,可以看到圆周率 import math import time r = 1000 ls_height = [] def circle_area(r, side
导数5:泰勒公式反观微积分
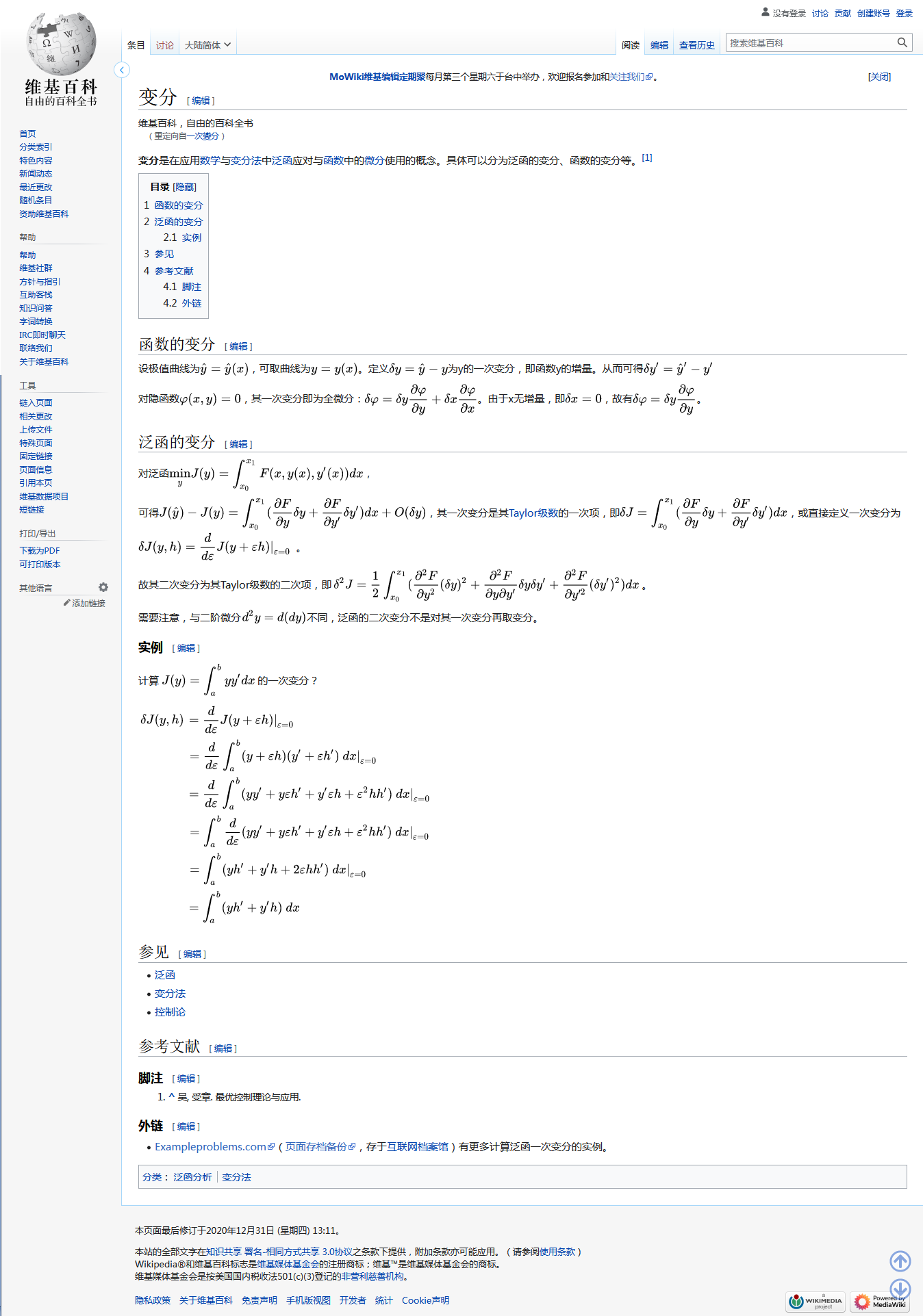
5-1.泛函反观 乌鸦喝水,当瓶子里的水少于0.259的比例时,填石子无法喝到水。 位置对时间求导就是速度 速度对时间求导就是加速度 对表达现函数与x轴所夹面积的函数求导可以得到表达函数(也就是原函数
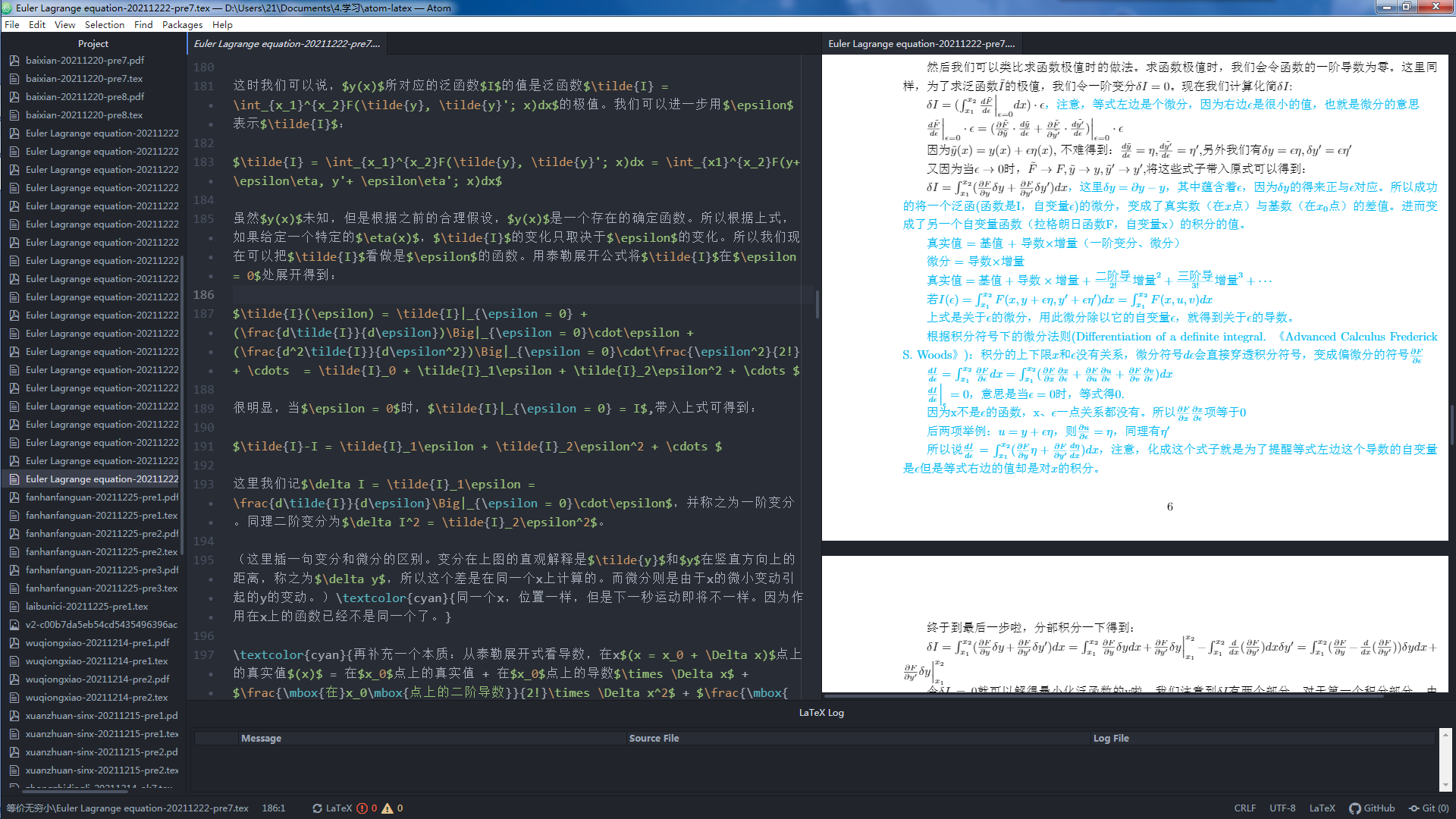
导数4:摆线、最速降线的原理推导:欧拉-拉格朗日定理
4-1.欧拉-拉格朗日方程 颜值举例-老狼老狼几点了 4-2.摆线、最速降线 下面是我这个月学到的最厉害的东西。用它可以证明以下一些日常的问题:1.两点之间直线最短。2.给定线段围出一个形状。如果想要
物理历史上的重要之路
最速降线——》费马原理——》变分法——》欧拉-拉格朗日方程 时间和空间都不存在,存在的只是运动。 磁场并不存在,因为有了电场,才有了磁场。磁铁的制造过程就是找稳定的原子集合成的物质加热,然后加高压电,
导数3:中值定理、泰勒展开、洛必达法则(罗尔中值定理证明拉格朗日中值定理时候的那些坑)、等价无穷小
柯西中值定理是拉格朗日中值定理的推广,是微分学的基本定理之一。其几何意义为,用参数方程表示的曲线上至少有一点,它的切线平行于两端点所在的弦。该定理可以视作在参数方程下拉格朗日中值定理的表达形式。 柯西
看到人生一片坦途的人也是一贫如洗
只有洞悉所有路障以及有本事迈过或者走出坑的人,才是人生赢家。
数学之路,重要的学习路径、学习路线有时候比学习方法、学习时间更重要
知道了乘法是快速的加法、重复的加法 知道了比例、投影是降维的产物 知道了圆周律 知道了自旋、极坐标转化成直角坐标 知道了傅里叶变换 知道了银行利率、自然对数 知道了复变函数 知道了复数域 重要的无理数