总结梳理的过程就是一个求大求全的过程
链接如下:数学的几条线 追求系统而不是追求结果。
顺时针、逆时针、左手系、右手系
没人给你串起来的的东西。我给你串。高等数学中定积分可以求面积。而闭合路径的面积以逆时针定义为正,是因为自变量x轴是从左到右并且因变量y轴是从下到上的。所以行列式的坐标鞋带法,就是正斜杠(矩阵中是列向量
vim 常用快捷键
vim 常用快捷键 动作:光标自己的行为 命令:完成一个屏幕、编辑器、功能等所需要的口令 操作:带参数的命令 光标的操作 h j k l 光标左移 :h 光标右移 :l 光标上移 :k 光标下移 :j
我的语文老师康老师交给了我
中心句不是一个自然段中,句号表示的最中间的那个句子。 下象棋的一篇文章中。谁是主角?不是最厉害的那个,而是描述用的字数最多的那个。对我来讲就是你这一生把时间花在最多的那个人和那个事儿,才是你生命中的主
三囚徒问题的概率统计python实现
三囚徒问题是一个经典的概率问题。假设有三个囚犯 A、B、C 被关在监狱中,他们中有一个人将要被处决,另外两个将要被赦免。狱卒告诉他们,其中一个门后面有救命的钥匙,而另外两扇门后面分别是死亡和赦免。狱卒
Monty Hall problem的概率统计python实现
这是一个众所周知的问题,许多人奇怪的直觉都难以正確回答。这個问题通常涉及到一個奖品放在三个门后,其中一个门后是奖品,另外两个门后是没有奖品的,门是关闭的。玩家必须选择一个门,然后主持人将会打開一个没有
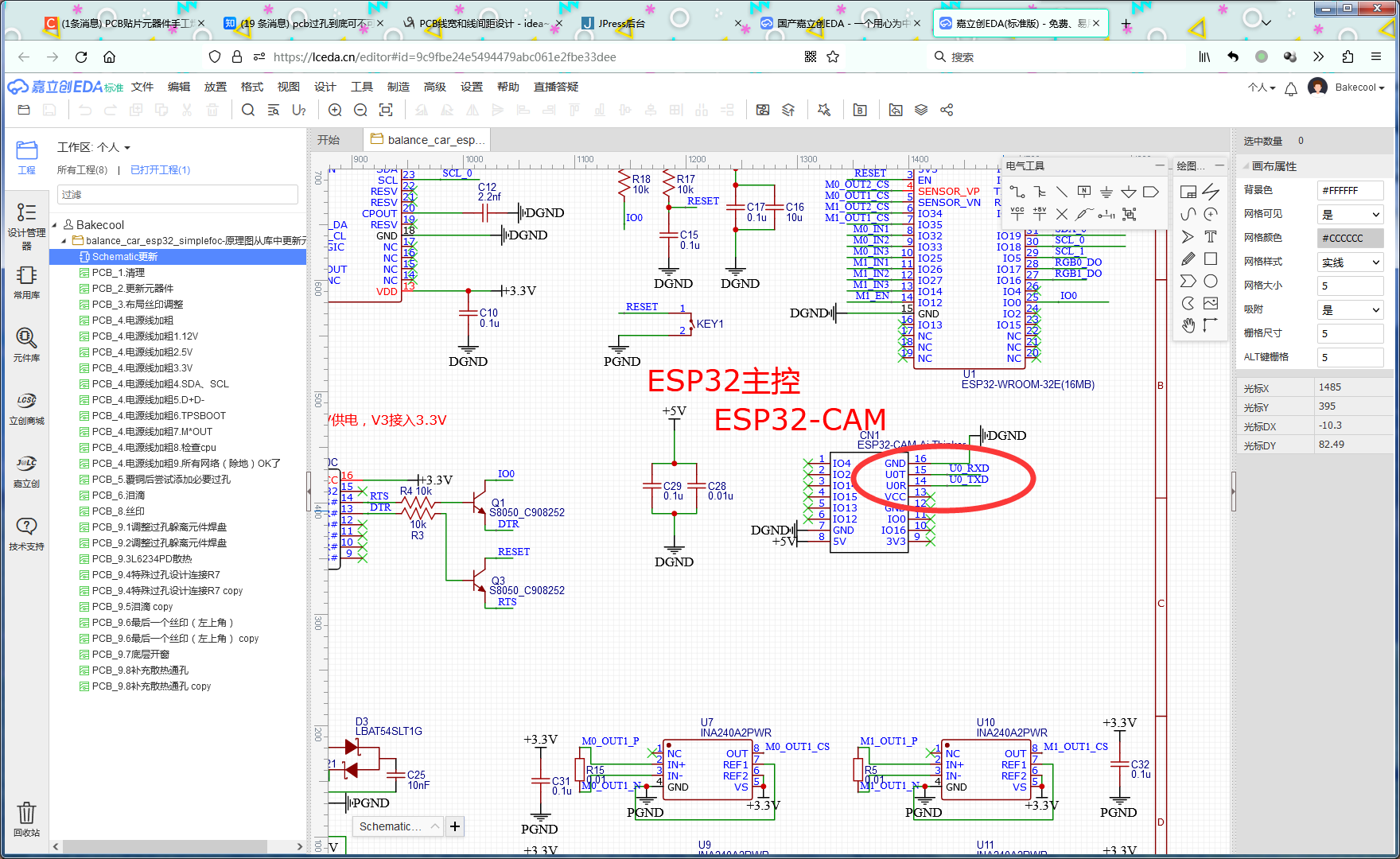
总结2022年9月自己画的电路板
首先来个文档学习线宽和线间距设计。 然后再说大的错误,虽然后续发现即使正确了也无法直接使用。 图中发送和接收的引脚在原理图时就画反了,导致在连线完毕后,实在没有力气想重新调整。但是后续发现,因为是5v
ChatGPT——用C++写一个求原根的程序
求素数和求原根 用C++写一个高效求原根的程序,要求:输入一个数字,输出该数字的所有原根到d盘的"yuangen.txt"文件,并给出详细注释。 下面是一个用C++编写的程序,用于
分毛驴问题
古时候有一位财主有11头驴,要求将其中的分给大儿子,其中的分给二儿子,再将其中的分给三儿子。在三个儿子一筹莫展的时候,一位骑驴而来的智者为他们“加进一头驴”而解决问题,你知道三个儿子分别分得多少头驴吗
虚数的意义,一元三次方程的求根公式
解决一元三次方程的解 文档 1545年,意大利学者卡丹(也翻译为卡尔达诺)(Cardano G.,1501-1576年)所著的《关于代数的大法》中给出了一元三次方程x³+px+q=0,(p,q∈R)的