python的安装路径
%appdata%(C:\Users\21\AppData\Roaming\Python\Python38) 和 C:\Users\21\AppData\Local\Programs
python运算符@重载
class Matrix: def __init__(self, matrix): self.values = matrix def __matmul__(self,
弹塑性力学引论-清华大学出版社 剪应力
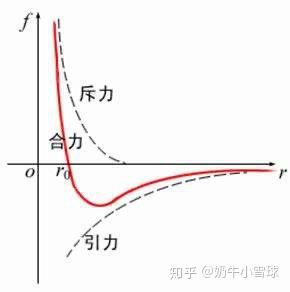
第三章有部分内容解释了应力张量,下面是 [hide] 总结 [/hide] 在分子相互远离的过程中,分子引力与斥力怎么变? python模拟
要教你的
跟我学习不用讲什么技法,讲求一个缘法。没必要课前预习、课后复习。没必要课后当一个小老师费曼学习,也没必要艾宾浩斯(H.Ebbinghaus)记忆曲线去巩固。我经历了完整的应试教育体系。在摧残的同时,我
latex常用符号
表向量:\overrightarrow{OA} 角度:60^{\circ} 求和:$\boldsymbol{\alpha} \bigcdot \boldsymbol{\beta} = \sum\lim
双射函数必为单调函数吗?
双射函数在每个连续的区间内,必为单调函数,但是在整个定义域内,不一定是单调函数。 例如函数f(x)=1/x,这个函数在x∈(-∞,0)∪(0,+∞)中都是双射函数,而且在(-∞,0)和(0,+∞)着两
证明矩阵的乘法具备乘法结合律
矩阵的乘法具备乘法结合律
映射、满射、单射、双射(注意学习的顺序)
什么叫映射?函数。就是一支箭射出去,一定会落在靶子上。不可能出现一支箭射出去,有两个靶子能够接住。比如射得不牢掉落又产生一个成绩。成绩只有一个,只看一个靶子的。叫做映射。一箭双雕?不存在的。 什么叫满
微分方程、微商、导数的顺序
既然导数是一个整体,那么如何理解微分方程中分离变量? 这是因为接触顺序的问题。 现在高数学习中,会先接触导数,后接触微分。 dy/dx可以拆分开,是要在接触微分之后才有意义,dy与dx分别表示函数的微
很全很常用的高中物理公式汇总
一、质点的运动(1) ------直线运动 1)匀变速直线运动 1.平均速度V平=s/t(定义式) 2.有用推论Vt2-Vo2=2as 3.中间时刻速度Vt/2=V平=(Vt+Vo)/2 4.末速度V