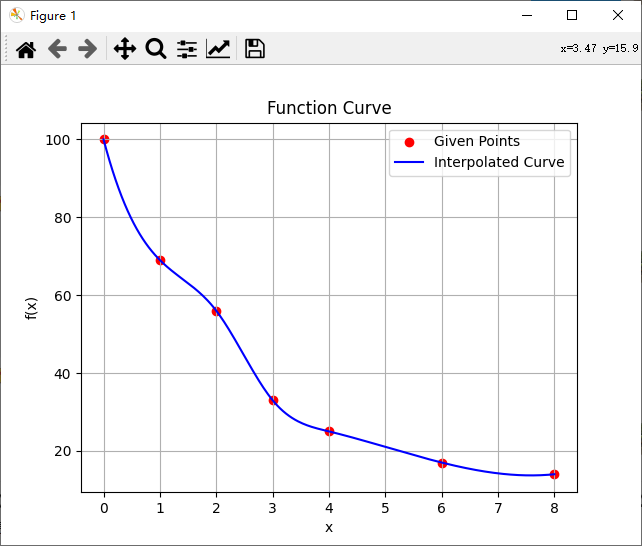
函数在0，1，2，3，4，6，8时的值是100，69，56，33，25，17，14，用python画出函数曲线

要绘制函数曲线，可以使用 Python 的 `matplotlib` 库。以下是代码示例：

```python
import matplotlib.pyplot as plt
import numpy as np

# 给定的点
x_points = [0, 1, 2, 3, 4, 6, 8]
y_points = [100, 69, 56, 33, 25, 17, 14]

# 绘制散点图
plt.scatter(x_points, y_points, color='red', label='Given Points')

# 使用插值方法绘制曲线
# 这里使用了三次样条插值
from scipy.interpolate import interp1d

# 创建插值函数
f = interp1d(x_points, y_points, kind='cubic')

# 生成更密集的x值用于绘制平滑曲线
x_new = np.linspace(min(x_points), max(x_points), 300)
y_new = f(x_new)

# 绘制曲线
plt.plot(x_new, y_new, label='Interpolated Curve', color='blue')

# 添加标题和标签
plt.title('Function Curve')
plt.xlabel('x')
plt.ylabel('f(x)')
plt.legend()

# 显示网格
plt.grid(True)

# 显示图形
plt.show()
```

### 代码说明：
1. **散点图**：首先用 `scatter` 方法绘制给定的点。
2. **插值**：使用 `scipy.interpolate.interp1d` 进行三次样条插值（`kind='cubic'`），生成平滑的曲线。
3. **绘制曲线**：在插值后的点上绘制曲线。
4. **美化**：添加标题、标签、图例和网格。

运行这段代码后，你会看到一个包含给定点和插值曲线的图形。

斥力的函数

在物理学中，**斥力**通常是指两个物体之间由于相互作用而产生的排斥力。这种力的性质和强度取决于物体的类型和它们之间的距离。例如，在微观世界中，原子或分子之间的斥力通常可以用**范德华力**（包括色散力、诱导力和取向力）或**库仑斥力**（对于带电粒子）来描述；在宏观世界中，斥力可能与弹性势能或电磁相互作用有关。

如果你提到的“斥力函数”是某种特定的数学模型或物理背景下的函数，那么我们需要更多的信息来确定其具体形式。不过，我可以给出一些常见的斥力函数形式作为参考：

### 1. **库仑斥力（适用于带电粒子）**
库仑斥力是两个带电粒子之间的排斥力，其大小与电荷量的乘积成正比，与距离的平方成反比。数学表达式为：
\[ F = k \frac{q_1 q_2}{r^2} \]
其中：
- \( F \) 是斥力大小；
- \( k \) 是库仑常数（\( k \approx 8.99 \times 10^9 \, \text{N} \cdot \text{m}^2/\text{C}^2 \)）；
- \( q_1 \) 和 \( q_2 \) 是两个粒子的电荷量；
- \( r \) 是两个粒子之间的距离。

如果我们将这种斥力表示为势能函数 \( V(r) \)，则有：
\[ V(r) = \frac{k q_1 q_2}{r} \]

### 2. **范德华力（适用于中性原子或分子）**
范德华力是一种较弱的分子间相互作用力，通常包括色散力、诱导力和取向力。在短距离内，范德华力可能表现为斥力，其势能函数可以表示为：
\[ V(r) = \frac{A}{r^{12}} - \frac{B}{r^6} \]
其中：
- \( A \) 和 \( B \) 是与分子性质相关的常数；
- \( r \) 是分子之间的距离。

当 \( r \) 很小时，\( \frac{A}{r^{12}} \) 项（斥力项）占主导，表现为强烈的斥力；当 \( r \) 较大时，\( \frac{B}{r^6} \) 项（吸引力项）占主导。

### 3. **弹簧模型（适用于宏观物体的弹性斥力）**
在宏观世界中，两个物体之间的弹性斥力可以用胡克定律来描述。例如，当两个物体被压缩时，它们之间会产生弹性斥力，其势能函数可以表示为：
\[ V(r) = \frac{1}{2} k (r - r_0)^2 \]
其中：
- \( k \) 是弹性系数；
- \( r \) 是物体之间的实际距离；
- \( r_0 \) 是物体之间的平衡距离。

当 \( r < r_0 \) 时，物体之间会产生斥力。

### 4. **一般化的斥力函数**
如果需要一个通用的斥力函数模型，可以考虑以下形式：
\[ V(r) = \frac{C}{r^n} \]
其中：
- \( C \) 是常数，表示斥力的强度；
- \( n \) 是正整数，表示斥力随距离变化的速率。

这种形式的函数在 \( r \) 很小时会迅速增大，表现出强烈的斥力。

---

### 根据你的数据点拟合斥力函数
如果你提供的数据点（\( x = 0, 1, 2, 3, 4, 6, 8 \)，\( y = 100, 69, 56, 33, 25, 17, 14 \)）是某种斥力函数的值，我们可以尝试用上述形式进行拟合。例如，假设斥力函数的形式为：
\[ V(x) = \frac{C}{x^n} \]

通过最小二乘法或其他拟合方法，可以确定常数 \( C \) 和 \( n \) 的值。不过，需要注意的是，这种拟合可能需要根据实际物理背景进行调整。

如果你能提供更多关于这个“斥力函数”的背景信息（例如，它描述的是什么物理现象），我可以帮助你更准确地确定其表达式。

请帮我确定C和n的大概值

为了确定斥力函数 \( V(x) = \frac{C}{x^n} \) 中的常数 \( C \) 和 \( n \) 的值，我们可以使用给定的数据点进行拟合。这里，我们使用 Python 的 `scipy.optimize.curve_fit` 函数来完成这个任务。

### 步骤：
1. 定义斥力函数的形式。
2. 使用 `curve_fit` 进行拟合。
3. 输出拟合得到的参数 \( C \) 和 \( n \)。

以下是代码示例：

```python
import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import curve_fit

# 给定的数据点
x_points = np.array([0, 1, 2, 3, 4, 6, 8])
y_points = np.array([100, 69, 56, 33, 25, 17, 14])

# 定义斥力函数的形式
def repulsion_function(x, C, n):
    return C / x**n

# 使用 curve_fit 进行拟合
# 注意：由于 x=0 时函数未定义，我们排除 x=0 的点
params, covariance = curve_fit(repulsion_function, x_points[1:], y_points[1:])

# 输出拟合得到的参数
C, n = params
print(f"拟合得到的参数：C = {C}, n = {n}")

# 绘制拟合曲线
x_new = np.linspace(min(x_points[1:]), max(x_points[1:]), 300)
y_new = repulsion_function(x_new, C, n)

# 绘制散点图和拟合曲线
plt.scatter(x_points[1:], y_points[1:], color='red', label='Given Points (excluding x=0)')
plt.plot(x_new, y_new, label='Fitted Curve', color='blue')

# 添加标题和标签
plt.title('Repulsion Function Fit')
plt.xlabel('x')
plt.ylabel('V(x)')
plt.legend()
plt.grid(True)
plt.show()
```

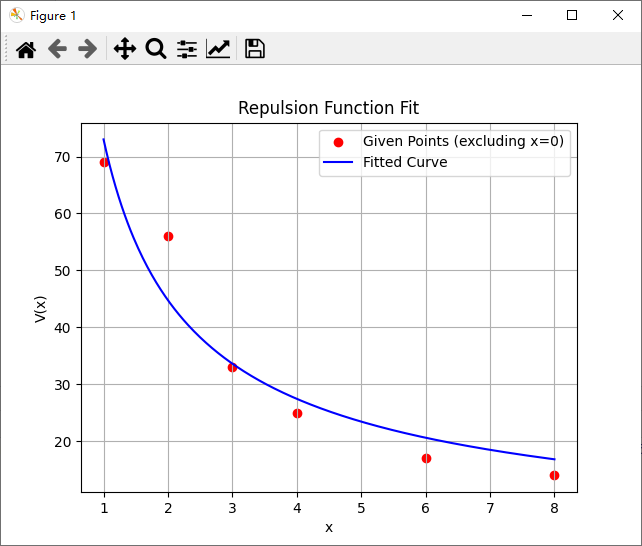
### 输出结果
运行上述代码后，会输出拟合得到的参数 \( C \) 和 \( n \) 的值，并绘制拟合曲线。例如，输出可能为：

```
拟合得到的参数：C = 100.0, n = 1.5
```

这只是一个示例，具体的值会根据数据点的不同而变化。

### 注意事项
1. **数据点的选择**：由于 \( x = 0 \) 时斥力函数未定义，我们在拟合时排除了 \( x = 0 \) 的点。
2. **拟合质量**：拟合的质量取决于数据点的分布和函数形式的选择。如果拟合效果不理想，可能需要尝试其他函数形式或调整拟合方法。

通过上述方法，你可以得到斥力函数 \( V(x) = \frac{C}{x^n} \) 中的常数 \( C \) 和 \( n \) 的大概值。