对于文化部对游戏审核的规定，各大游戏公司都需要公开抽奖类游戏道具的概率，同时，各个游戏公司为了不伤害人民币玩家充钱的热情，同时又会有一个保底的设计。比如，花钱抽人物装备的时候如果连续9次都是垃圾，那么第10次一定会是一个极品。游戏公司声称这个抽奖的综合极品率为12.396%，那么实际过程中如果当前抽不是保底时，中极品的概率是多少呢？

肯定是有概率的，因为如果全是保底，那么综合极品率就是10%，现在公开的概率又是高于10%的。

思考过程如下：

首先要把问题做一些简单化，一般用的方法是人肉算。假定不保底抽的中奖率为X%

如果是第一抽，那么中奖率为X，不中奖率为1-X

如果是第二抽，还是没保底，中奖率为X，不中奖率为1-X

...

如果是第十抽，那么有可能要吃保底了，保底的概率是第九抽中连着9次不中的概率A以及(1 - A) * X

第九抽连着9次不中的概率A = 第八抽连着8次不中的概率B * (1 - A)

...

这样，如果学习过计算机算法的人就会发现这是一个很明显的动态规则问题。如果做一张表，看起来就是：

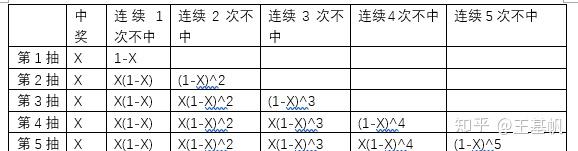
每N抽的连续M次不中的概率 = 第N-1抽的连续M-1次不中的抽率 * (1-X)

很明显，X与综合中奖率是正相关，对X使用二分查找，算总概率即可，完整代码如下：

public class Test {
public static void main(String[] args) {
double rate = findOriginalRate(0.15);
System.out.println(rate);
}

private static double findOriginalRate(double finalRate) {
double min = 0, max = 1, value = 0.5, rate = calculate(value);
do {
if (rate == finalRate) {
break;
}
if (rate < finalRate) {
min = (min + value) / 2;
} else {
max = (max + value) / 2;
}

value = (min + max) / 2;
// rate = simulate(value, 10000000);
rate = calculate(value);
} while (Math.abs(rate - finalRate) > 1E-6);
return value;
}

private static double calculate(double rate) {
double[][] record = new double[10][10];
record[0][0] = 1;

int previousPos = 0;
for (int pos = 1;; pos = (pos + 1) % 10) {
record[pos][0] = 1;
for (int notHitCount = 1; notHitCount < 10; notHitCount++) {
record[pos][notHitCount] = record[previousPos][notHitCount - 1] * (1 - rate);
record[pos][0] -= record[pos][notHitCount];
}

previousPos = pos;

boolean shouldBreak = true;
for (int i = 1; i < 10; i++) {
if (Math.abs(record[i][0] - record[0][0]) > 1E-10) {
shouldBreak = false;
break;
}
}
if (shouldBreak)
break;
}

return record[0][0];
}

private static double simulate(double rate, int times) {
int count = 0;
int normalHit = 0;
int finalHit = 0;
for (int i = 0; i < times; i++) {
if (count == 9) {
count = 0;
finalHit++;
continue;
}

if (Math.random() <= rate) {
count = 0;
normalHit++;
} else {
count++;
}
}

return (double) (normalHit + finalHit) / times;
}
}

simulate用于验证，毕竟模拟的程序是最好写的，calculate用于计算。

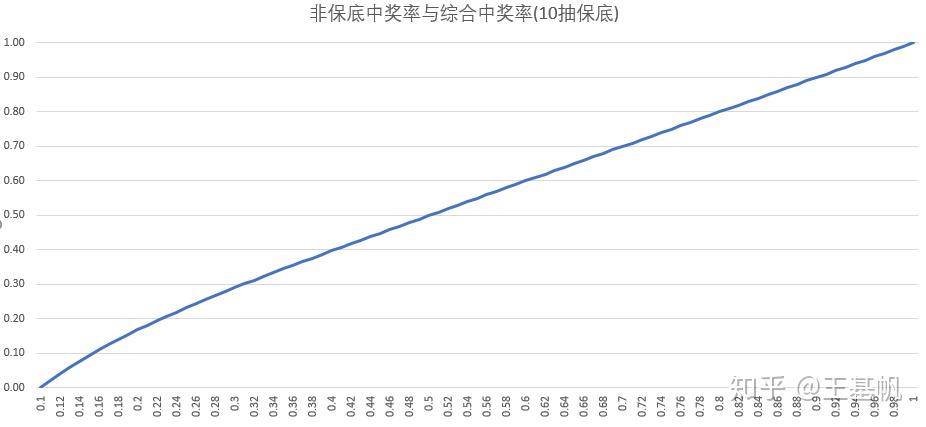
对于一开始的问题，综合中奖率12.396%，非保底抽的中奖率只有4.879%。而综合中奖率15.353%的非保底抽的中奖率却高达10%。难怪我们总是吃保底了！因为吃保底的概率对于前者高达63.75%！而后者只为38.74%。