推论：二维空间内。相似形状的面积比，等于形状（任意段）外周长或形状内连接线的比的平方

1672 2021-02-04 09:21

二维就是平方、三维就是立方。

一维就是匀速直线运动。由点产生的直线。

相似图形的面积比例为边长比的平方。

求证，你往一个瓶子里面装玻璃球，要求玻璃球的直径相等。则装满后填满水，那么不管你玻璃球的直径是多大或者多小，填满的水永远是相同的多。

来自知乎：

先放结论：
乌鸦能不能喝到水，与瓶子形状关系不大，主要取决于里面有多少水、石子形状、石子级配。

如果它扔的都是一模一样的圆球，球是否越小越好？
球的大小对结果影响不大。球小了，孔隙体积与固体体积的比例并不会变。这句话并不绝对，如果石子直径比较大，边界影响不能忽略，大小对结果有一定影响。

间接推论：已知相似比例，以及两边，第三边可求。

证明方法：面积都能切割成三角形。微分三角形之后。有余弦定理

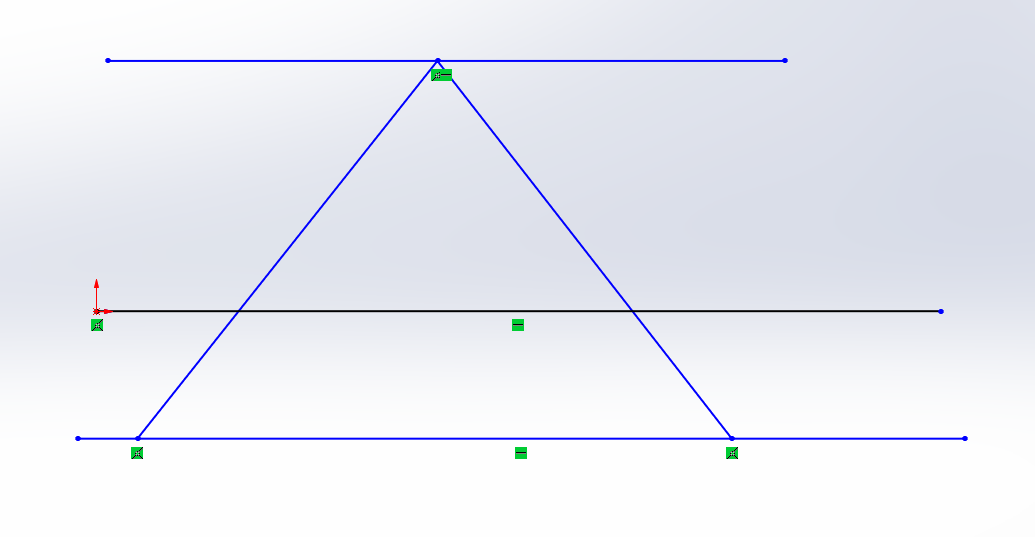
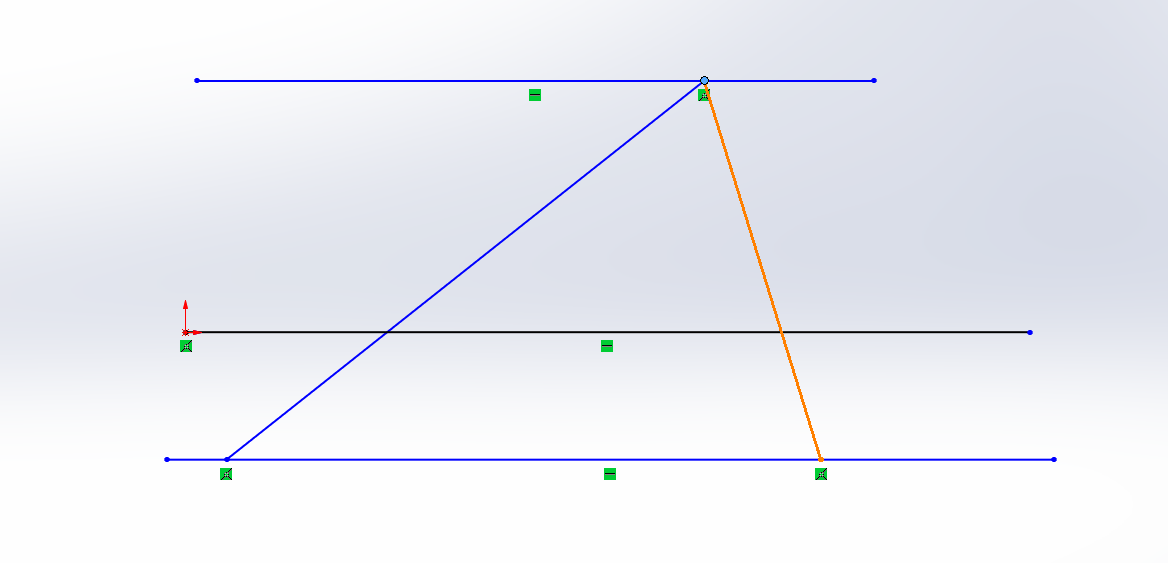
或者由微分曲线可知，面积由小矩形微分组成。那么底乘以高就是面积。而高在y=f(x)中由x决定，那么x*f(x)中，x变化，那么面积也就是x平方的函数。

博客