转发:PID算法终于弄明白原理了,原来就这么简单
5328 2020-05-22 13:11
废话不多说,先看东西:
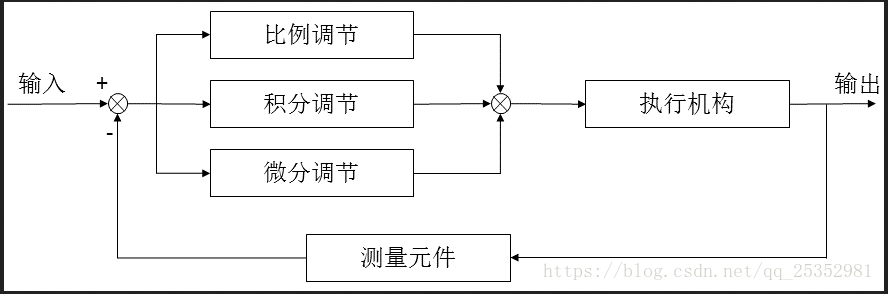

PID算法终于弄明白原理了,原来就这么简单
原文:https://www.cnblogs.com/whylinux/p/10960319.html
看起来PID高大尚,实则我们都是被他的外表所震撼住了。先被别人唬住,后被公式唬住,由于大多数人高数一点都不会或者遗忘,所以再一看公式,简直吓死。了解了很浅的原理后,结果公式看不懂,不懂含义,所以最终没有透彻。我这里先对公式进行剖析,公式理解明白了,结合网上的一些pid讲述的例子,就明白了。
先对PID这三个系数的含义进行简单扫盲,。同时也防止自己遗忘。P是比例系数,I是积分系数、D是微分系数。下面对PID这三个系数进行详细说明。
1.比例系数P是干什么用,其实如果现在你是初中生的话,你一下子就懂了,比例系数就是用在穿过(0,0)这个坐标点直线的放大倍数k,k越大,直线的斜率越大,所以是用在y = k * x中的,其中的k就是比例系数p,大家都简称为kp,所以就变成了y = Kp * x。
x就是当前值currentValue和目标值totalValue的差值,简称误差err,则err = currentValue - totalValue。y就是执行器对应的输出值U,所以执行器对应的输出值U = Kp * ( currentValue - totalValue ) 。
所以,如果说是使用比例进行调节。
则当前第1次调节时执行器对应的输出值为U1 = Kp * ( curentValue1 - totalValue1 )。
第2次调节时执行器对应的输出值为U2 = Kp * ( currentValue2 - totalValue2 )。
这就是比例系数P的应用,也就是大家说的比例调节。比例调节就是根据当前的值与目标值的差值,乘以了一个Kp的系数,来得到一个输出值,这输出值直接影响了下次当前值的变化。如果只有比例调节的话,系统会震荡的比较厉害。比如你的汽车现在运行的速度是60km/h,现在你想通过你的执行器去控制这个汽车达到恒定的50km/h,如果你只用kp进行比例调节话。U = Kp * ( 60 - 50 ),假设Kp取值为1,此时得到U执行器的输出值是10,结果当你执行器输出后,发现汽车一下变成了35Km/h,此时U2 = Kp * (35 - 50),此时得到U执行器的输出值是-15,结果当你执行器输出后,发现汽车变成了55Km/h,由于惯性和不可预知的误差因素,你的汽车始终无法达到恒定的50km/h。始终在晃动,相信如果你在车上,你一定吐的很厉害。所以光有比例系数进行调节,在有些场合是没有办法将系统调稳定的。所以可以为了减缓震荡的厉害,则会结合使用比例P和微分D。
2.微分系数D
微分,实际上是对误差进行微分。加入误差1是err(1)。误差2是err(2)。则误差err的微分是 (err2 - err1)。乘上微分系数D,大家叫做KD,则当执行器第1次调节后有了第1次的误差,第2次调节后有了第2次的误差,则结合P系数。就有了PD结合,根据每次调节时,误差的值的经验推算,你就能选取出D的系数。假如误差是越来越小的,那么微分后肯定是一个负值。负值在乘以了一个D系数 加上了比例调节的值后肯定值要比单纯使用比例调节的值要小,所以就启到了阻尼的作用。有了阻尼的作用就会使得系统区域稳定。PD结合的公式经过上面的分析后为
U(t) = Kp * err(t) + Kd * derr(t)/dt
3.积分系数I
积分,实际上是对误差的积分,也就是误差的无限和。如何理解积分系数I,这里引用网上的例子
以热水为例。假如有个人把我们的加热装置带到了非常冷的地方,开始烧水了。需要烧到50℃。
在P的作用下,水温慢慢升高。直到升高到45℃时,他发现了一个不好的事情:天气太冷,水散热的速度,和P控制的加热的速度相等了。
这可怎么办?
P兄这样想:我和目标已经很近了,只需要轻轻加热就可以了。
D兄这样想:加热和散热相等,温度没有波动,我好像不用调整什么。
于是,水温永远地停留在45℃,永远到不了50℃。
作为一个人,根据常识,我们知道,应该进一步增加加热的功率。可是增加多少该如何计算呢?
前辈科学家们想到的方法是真的巧妙。
设置一个积分量。只要偏差存在,就不断地对偏差进行积分(累加),并反应在调节力度上。
这样一来,即使45℃和50℃相差不太大,但是随着时间的推移,只要没达到目标温度,这个积分量就不断增加。系统就会慢慢意识到:还没有到达目标温度,该增加功率啦!
到了目标温度后,假设温度没有波动,积分值就不会再变动。这时,加热功率仍然等于散热功率。但是,温度是稳稳的50℃。
kI的值越大,积分时乘的系数就越大,积分效果越明显。
所以,I的作用就是,减小静态情况下的误差,让受控物理量尽可能接近目标值。
I在使用时还有个问题:需要设定积分限制。防止在刚开始加热时,就把积分量积得太大,难以控制。
所以最终结合PID后,公司就变成了,本人直接从网上找了截图如下
一文读懂PID控制算法(抛弃公式,从原理上真正理解PID控制)
原文:https://blog.csdn.net/qq_25352981/article/details/81007075?utm_source=blogxgwz0
PID控制应该算是应用非常广泛的控制算法了。小到控制一个元件的温度,大到控制无人机的飞行姿态和飞行速度等等,都可以使用PID控制。这里我们从原理上来理解PID控制。
PID(proportion integration differentiation)其实就是指比例,积分,微分控制。先把图片和公式摆出来,看不懂没关系。(一开始看这个算法,公式能看懂,具体怎么用怎么写代码也知道,但是就是不知道原理,不知道为什么要用比例,微分,积分这3个项才能实现最好的控制,用其中两个为什么不行,用了3个项能好在哪里,每一个项各有什么作用)
PID控制算法原理
PID控制算法公式
总的来说,当得到系统的输出后,将输出经过比例,积分,微分3种运算方式,叠加到输入中,从而控制系统的行为,下面用一个简单的实例来说明。
比例控制算法
我们先说PID中最简单的比例控制,抛开其他两个不谈。还是用一个经典的例子吧。假设我有一个水缸,最终的控制目的是要保证水缸里的水位永远的维持在1米的高度。假设初试时刻,水缸里的水位是0.2米,那么当前时刻的水位和目标水位之间是存在一个误差的error,且error为0.8.这个时候,假设旁边站着一个人,这个人通过往缸里加水的方式来控制水位。如果单纯的用比例控制算法,就是指加入的水量u和误差error是成正比的。即
u=kp*error
假设kp取0.5,
那么t=1时(表示第1次加水,也就是第一次对系统施加控制),那么u=0.5*0.8=0.4,所以这一次加入的水量会使水位在0.2的基础上上升0.4,达到0.6.
接着,t=2时刻(第2次施加控制),当前水位是0.6,所以error是0.4。u=0.5*0.4=0.2,会使水位再次上升0.2,达到0.8.
如此这么循环下去,就是比例控制算法的运行方法。
可以看到,最终水位会达到我们需要的1米。
但是,单单的比例控制存在着一些不足,其中一点就是 –稳态误差!(我也是看了很多,并且想了好久才想通什么是稳态误差以及为什么有稳态误差)。
像上述的例子,根据kp取值不同,系统最后都会达到1米,不会有稳态误差。但是,考虑另外一种情况,假设这个水缸在加水的过程中,存在漏水的情况,假设每次加水的过程,都会漏掉0.1米高度的水。仍然假设kp取0.5,那么会存在着某种情况,假设经过几次加水,水缸中的水位到0.8时,水位将不会再变换!!!因为,水位为0.8,则误差error=0.2. 所以每次往水缸中加水的量为u=0.5*0.2=0.1.同时,每次加水缸里又会流出去0.1米的水!!!加入的水和流出的水相抵消,水位将不再变化!!
也就是说,我的目标是1米,但是最后系统达到0.8米的水位就不在变化了,且系统已经达到稳定。由此产生的误差就是稳态误差了。
(在实际情况中,这种类似水缸漏水的情况往往更加常见,比如控制汽车运动,摩擦阻力就相当于是“漏水”,控制机械臂、无人机的飞行,各类阻力和消耗都可以理解为本例中的“漏水”)
所以,单独的比例控制,在很多时候并不能满足要求。
积分控制算法
还是用上面的例子,如果仅仅用比例,可以发现存在暂态误差,最后的水位就卡在0.8了。于是,在控制中,我们再引入一个分量,该分量和误差的积分是正比关系。所以,比例+积分控制算法为:
u=kp*error+ ki∗∫
error
还是用上面的例子来说明,第一次的误差error是0.8,第二次的误差是0.4,至此,误差的积分(离散情况下积分其实就是做累加),∫
error=0.8+0.4=1.2. 这个时候的控制量,除了比例的那一部分,还有一部分就是一个系数ki乘以这个积分项。由于这个积分项会将前面若干次的误差进行累计,所以可以很好的消除稳态误差(假设在仅有比例项的情况下,系统卡在稳态误差了,即上例中的0.8,由于加入了积分项的存在,会让输入增大,从而使得水缸的水位可以大于0.8,渐渐到达目标的1.0.)这就是积分项的作用。
微分控制算法
换一个另外的例子,考虑刹车情况。平稳的驾驶车辆,当发现前面有红灯时,为了使得行车平稳,基本上提前几十米就放松油门并踩刹车了。当车辆离停车线非常近的时候,则使劲踩刹车,使车辆停下来。整个过程可以看做一个加入微分的控制策略。
微分,说白了在离散情况下,就是error的差值,就是t时刻和t-1时刻error的差,即u=kd*(error(t)-error(t-1)),其中的kd是一个系数项。可以看到,在刹车过程中,因为error是越来越小的,所以这个微分控制项一定是负数,在控制中加入一个负数项,他存在的作用就是为了防止汽车由于刹车不及时而闯过了线。从常识上可以理解,越是靠近停车线,越是应该注意踩刹车,不能让车过线,所以这个微分项的作用,就可以理解为刹车,当车离停车线很近并且车速还很快时,这个微分项的绝对值(实际上是一个负数)就会很大,从而表示应该用力踩刹车才能让车停下来。
切换到上面给水缸加水的例子,就是当发现水缸里的水快要接近1的时候,加入微分项,可以防止给水缸里的水加到超过1米的高度,说白了就是减少控制过程中的震荡。
现在在回头看这个公式,就很清楚了
这里写图片描述
括号内第一项是比例项,第二项是积分项,第三项是微分项,前面仅仅是一个系数。很多情况下,仅仅需要在离散的时候使用,则控制可以化为
这里写图片描述
这里写图片描述
每一项前面都有系数,这些系数都是需要实验中去尝试然后确定的,为了方便起见,将这些系数进行统一一下:
这里写图片描述
这样看就清晰很多了,且比例,微分,积分每个项前面都有一个系数,且离散化的公式,很适合编程实现。
讲到这里,PID的原理和方法就说完了,剩下的就是实践了。在真正的工程实践中,最难的是如果确定三个项的系数,这就需要大量的实验以及经验来决定了。通过不断的尝试和正确的思考,就能选取合适的系数,实现优良的控制器。


全部评论