牛二：F=ma

其中m是物质的属性：质量。a是反应速度变化的效果，是位置在时间上的二阶导数。力是一种配合物质和效果的看不见摸不着，但是因地制宜逐个对待的却又可以统一计算的能量。E=FS

欧拉拉格朗日方程中，拉格朗日函数

以下摘自百度--------------：

 拉格朗日函数是在力学系上只有保守力的作用，是描述整个物理系统的动力状态的函数

 蚂蚁木板斜角度的正方形变形——度规张量（Metric Tensor）——微分流形

拉格朗日函数\mathcal{L}=\mathcal{T}-\mathcal{V}、欧拉-拉格朗日方程

这里其实叫做拉格朗日量，而拉格朗日量对应时间变量产生的积分，才是一个作用量的泛函。L是一个个变量（参数）对应的一个个值，而S是一个具体的值。S是能量，L是效果。

一个物理系统的作用量\mathcal{S}是一种泛函，以数学方程定义为

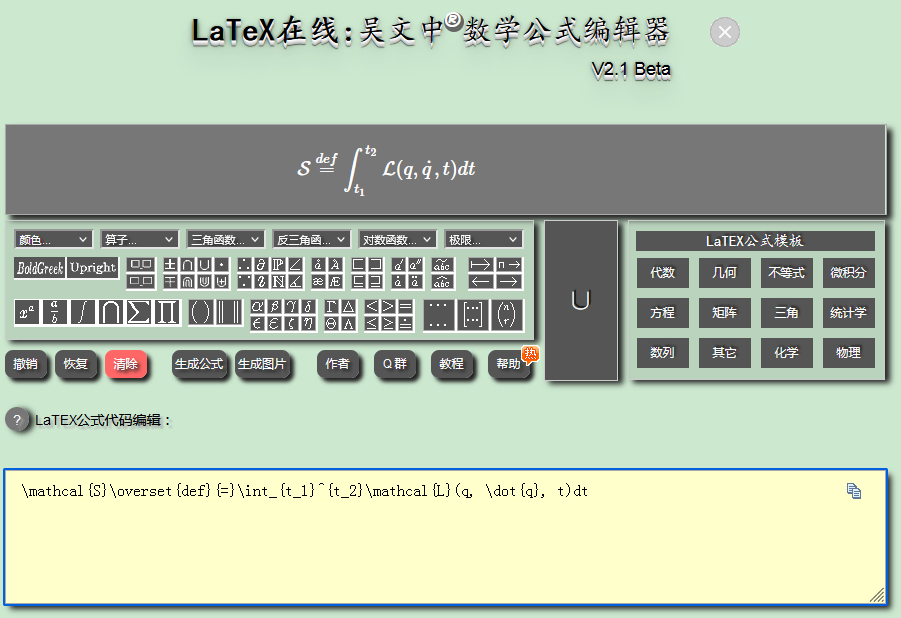
所谓q(t)正确地描述这物理系统的真实演化，就是说，不管时间段内来自各方的力如何施加，物体表现出的运动轨迹，都将是合力所产生的效果。那么位置、速度、时间所对应的函数“拉格朗日函数”在这个时间段上的积分，就将是该时间段的作用量，注意这里是作用量，体现了作用和量化两方面。作用量的微分

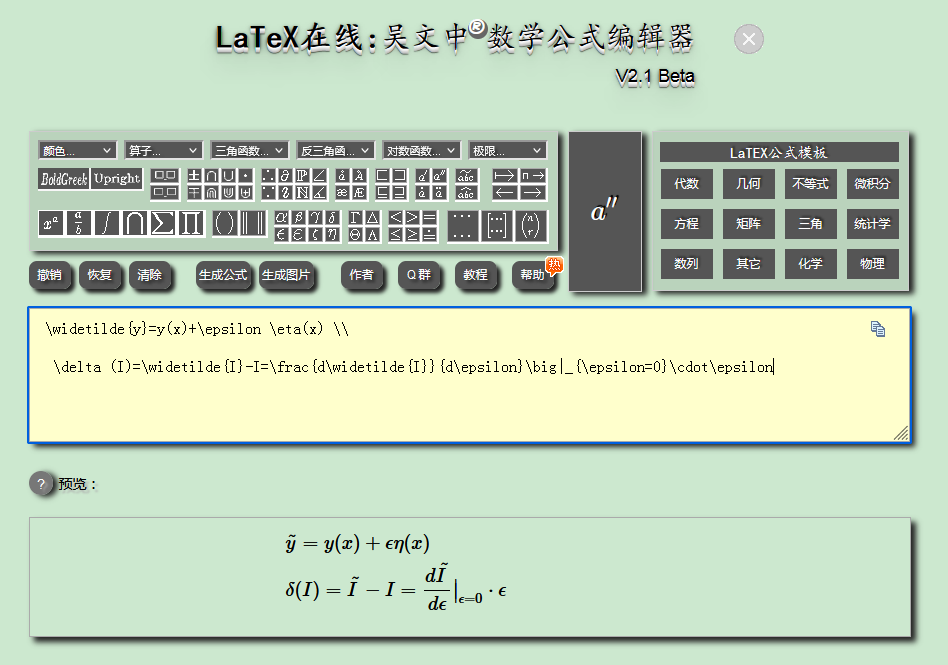
\widetilde{I}的变化，只取决与\epsilon

field属性描述的是状态，不变的；methord方法描述的是过程是变化，是一系列用的力造成的现象、效果、操作过程。比如将蓝球染成红球，球的属性颜色，经历了染这个方法，从蓝色变成了红色。

字段属性就是没有力的匀速直线运动，或静止的惯性系下的物体的运动状态的描述。可能就是一个速度、质量。

我有一个能量球，我把它当包子吃进肚子。带给我左右手各有一次发六脉神剑的能力。在我两手之间有一个小球，我左手弹了一下F*S，小球获得速度(1/2)mv^2，右手弹了一下(-F*S)，小球从左边停止到了右边。我左手弹了一下，右手顺势弹了一下，小球跑向了右边远处。我吃了好几个包子，上下左右弹小球，小球在我怀抱中各种运动。最后停止。这个过程中我使用的能量产生了各种位置变化的效果。但是，如果我能量固定，那么这能量让小球最远的运动效果，只有一直顺势去弹小球。反过来。小球运动的顺势趋势就是这四维欧氏空间的直线，而最小作用量产生的效果，也就是直线。所以两点之间直线最短。可能学小学、初中的人不知道为什么这里不说线段最短。以上就是原因。但是除了物理学相关专业人士。大部分人是不理解上述思维的。

最速降线和势能有关，那么直线的推导为什么要看势能？