导数4:摆线、最速降线的原理推导:欧拉-拉格朗日定理
11979 2021-12-26 10:05 2022-06-08 08:31
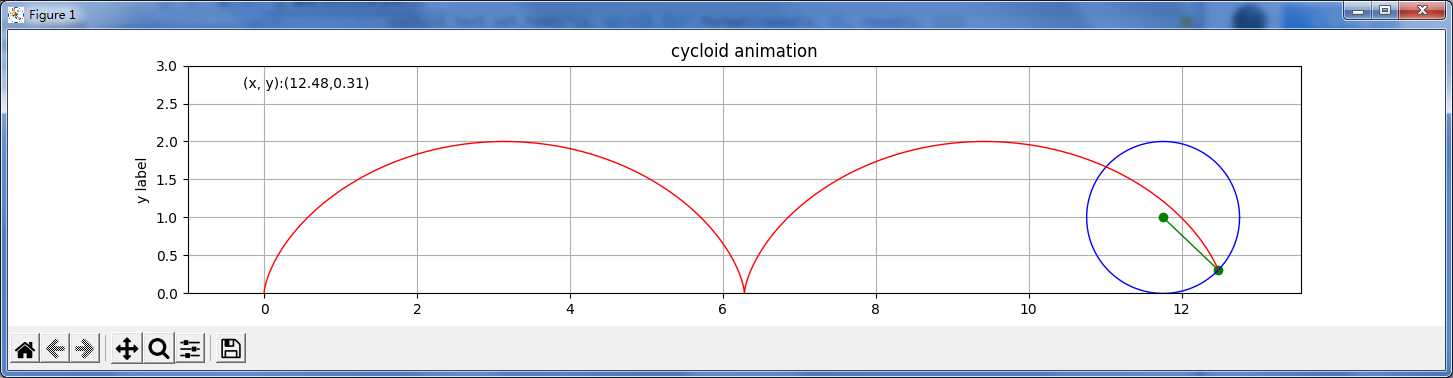
下面是我这个月学到的最厉害的东西。用它可以证明以下一些日常的问题:1.两点之间直线最短。2.给定线段围出一个形状。如果想要最大的面积,那么这个形状一定是圆形。3.有一个小球向下方掉落,但是终点不能垂直正下方,那么小球到下落点的最快路径是一条摆线。在该摆线的任意位置放置静止的小球,那么这些小球将同时落到终点。(最速降线问题、摆线问题、等时降落问题)。4.光总是走最快的路线,光走的都是捷径(折射原理)。昨天举的那个例子叫最小作用量原理,也叫平稳作用量原理。是侦探小说里面反推理,也就是柯南说的“真相只有一个”的数学理论支撑。
欧拉-拉格朗日方程的意义在于对泛函:自变量是函数、因变量是值。定义域是函数集、值域是数集。 泛函也可以说是从向量空间到标量的一个映射。
经典力学中讨论(非量子场论):可拆分自变量比如x轴、y轴、z轴、t轴,只研究x轴的位移,综合其他:y、z轴,即可得到完整路径和起止点。
这里的函数集是一个三维空间加时间运动的小球,譬如在x轴上,依赖位置和速度的函数(拉格朗日函数)。这个函数和时间有关。从某一刻到另一刻。小球选择的路径。与作用量相关。如果作用量变化。那么小球选择的路径一定会变化(因为每个时间点都会对应不同的拉格朗日值,拉格朗日值代表当前功率)。这个作用量是位置和速度的函数在路径选择上的定积分。这个作用量的函数值就是泛函的值,作用量所依赖的两个函数就是泛函的自变量。
用拉格朗日函数求作用量是一种泰勒近似,但是边界条件在两点间最短路径是直线上都是0.所以又不是近似。
当作用量函数的斜率为0时,对小球所做的总功为0.也就是小球从停止开始运动,到停止运动结束之间。让小球动起来和停下来的总作用互相抵消了。这个0,和小球的起点终点没有关系。与路径无关。
拉格朗日函数关于时间的积分,导致着该运动物体总势能减去总动能的差值所表示的能量的变化。路径之所以改变,正是因为关于x轴的作用量改变了。功W=FS。其中s就是X轴的位置。这个作用量和时间可以脱钩。体现在力道。好现实的一个公式。好有用。但是拉格朗日是功率,体现在每个拉格朗日值的时候,会产生不同的路径(不同的位置和速度函数有可能产生相同的拉格朗日值,但此种情况下他们的斜率不同)。体现在时间上就是做了多少功。当功率为0的时候,也就是小球静止的时候。当功率斜率为0的时候,将会产生欧拉-拉格朗日方程。
原文:在我们定义的物理定律中,总功取决于系统的初始状态和最后状态,和它们之间的路径无关,那么系统的实际路径必须在该图的斜率为0的点处。斜率可以为0的地方是作用量最小的地方。因此,人们经常把这种求路径的方法称为“最小作用量原理”。但是可以更准确的称为“平稳作用量原理”,这时因为其真实路径应该在这些斜率为0的点上。
有了拉格朗日函数对于x轴位置的偏导数、有了拉格朗日函数对于速度(也就是关于时间)的偏导数。这里因为涉及到x、x关于时间(也就是速度),
对于一个刚性小球在一个惯性系下班位置相对的变化可以反映出唯一的整个过程的受力情况。那么拉格朗日函数就是一个功率函数。做功与动能的转化。小球位置和路径的变化都可以是唯一对应拉格朗日函数形状去态的。
拉格朗日方程
拉格朗日力学中,运动方程由 n {\displaystyle n} 
d d t ∂ L ∂ q i ˙ − ∂ L ∂ q i = Q i {\displaystyle {\mathrm {d} \over \mathrm {d} t}{\partial {\mathcal {L}} \over \partial {\dot {q_{i}}}}-{\partial {\mathcal {L}} \over \partial q_{i}}=Q_{i}} 
其中 Q i {\displaystyle Q_{i}} 

拉格朗日方程的地位等同于牛顿力学中的牛顿第二定律。但具有更普遍的意义。这个方式的解是经典解,在量子体系下,经典路径将不再是唯一路径。
最小作用量原理可以推出 两点之间直线最短、摆线、牛二、物体的质量等重要结论。
简谐运动包含了两个神奇的现象,一个是可以定义弹簧下的质量,一个是可以定义单摆的周期和质量、振幅无关。

全部评论