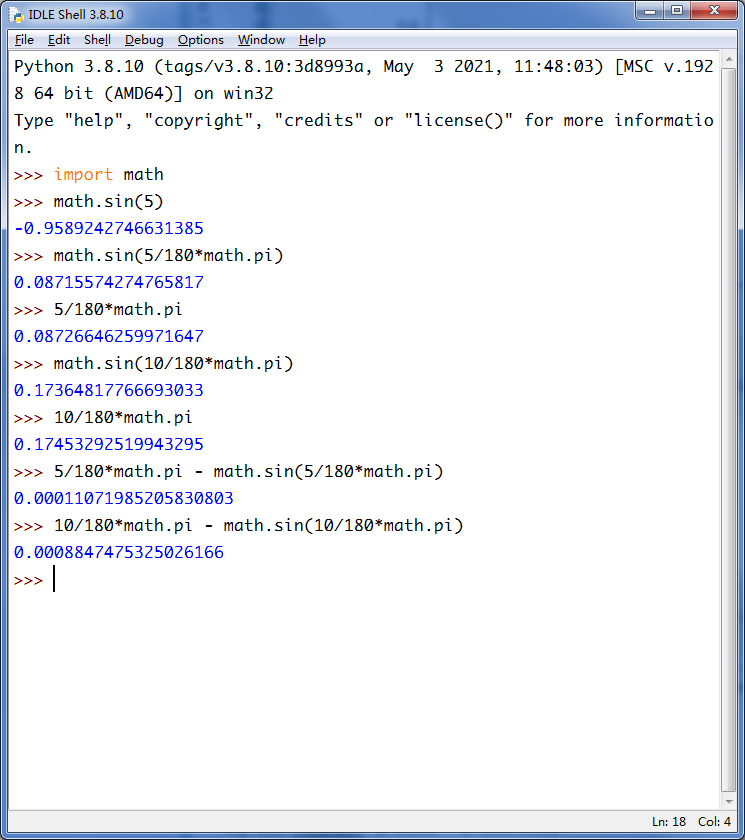
双缝干涉实验
参考知乎如何自己完成一个光的双缝干涉实验? 贾明子 做双缝干涉,需要考虑几个不同的因素: 1、光的相干性要好(单色),光强度要足够。这个容易实现,买一个大功率激光笔就行了。 2,缝隙的宽度要足够窄。
时空流形光滑才会导致质量电子的量子化吗?
是不是不知道说的啥。 就是物质属性之一,质量,是靠电子的随机位置撑起的。那么这种随机和跳跃出现,这种不连续,是因为我们假定了时空的连续吗? 你这个说法倒是很开拓思路,其实离散化在人脑经验来看就是没有因
马克思主义
马克思主义哲学是辩证唯物主义和历史唯物主义的统称,其前身是德国古典哲学。辩证唯物主义认为:世界的统一性在于它的物质性,物质是世界所发生的一切变化的基础。运动是物质的存在形式,物质的运动是绝对的,静止是
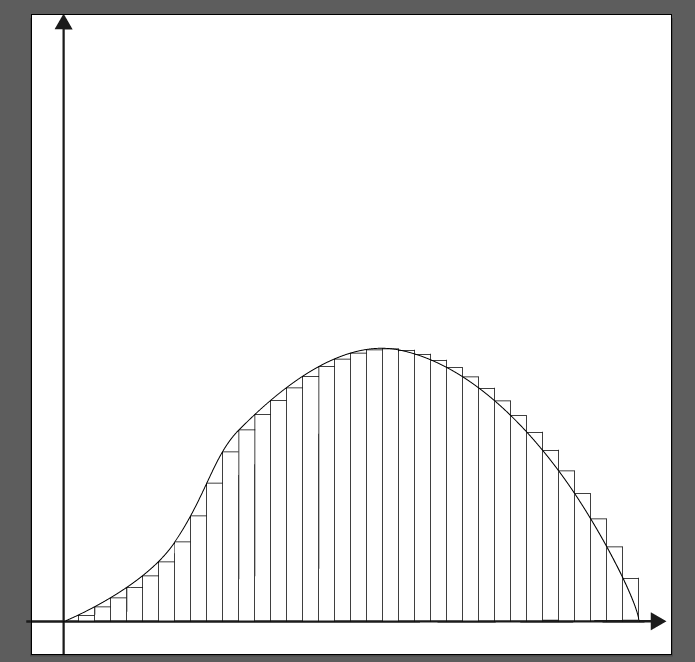
微积分用柱状图填充曲线到X轴的面积演示
填充柱状图
由“有朋自远方来”到“简单是福”
《一句顶一万句》老汪解释论语“有朋自远方来,不亦乐乎”。说正是圣人之悲。若是有贴心知己在身边,话都说尽了,远方来个朋友,岂不是白白添堵。况且并不知是不是朋友。这种辩证的思维,两级中庸的想法。也经常萦绕
角速度换算
rad/s:(弧度每秒 rad per second) deg/s:(角度每秒 degree per second) rpm:(转每分钟 RevolutionsPerMinuter) 把圆周的1/36
LQR的python程序,结果和matlab一致
[hide] LQR算法python版 [/hide]
python使用Control库进行LQR解算
conda create -n LQRControl python=3.8.10 激活使用 C:\Users\21> conda activate LQRControl (LQRControl