中国象棋子力值计算
我给出了preeval.cpp里面1到12的子力位置价值表 你给出的这些数组,是中国象棋 评估函数(evaluation function) 中的 “位置值表”(Position Value Tabl
变量、类型、对象、左值引用、右值引用
编程语言中的变量、类型、对象、右值、引用都是什么意思,有什么关联 下面把这些看似“散”的概念串成一条线,用一句话先给出总关系,再分层展开。 一句话总览 “变量”是具名存储槽;“类型”决定这个槽怎么解释
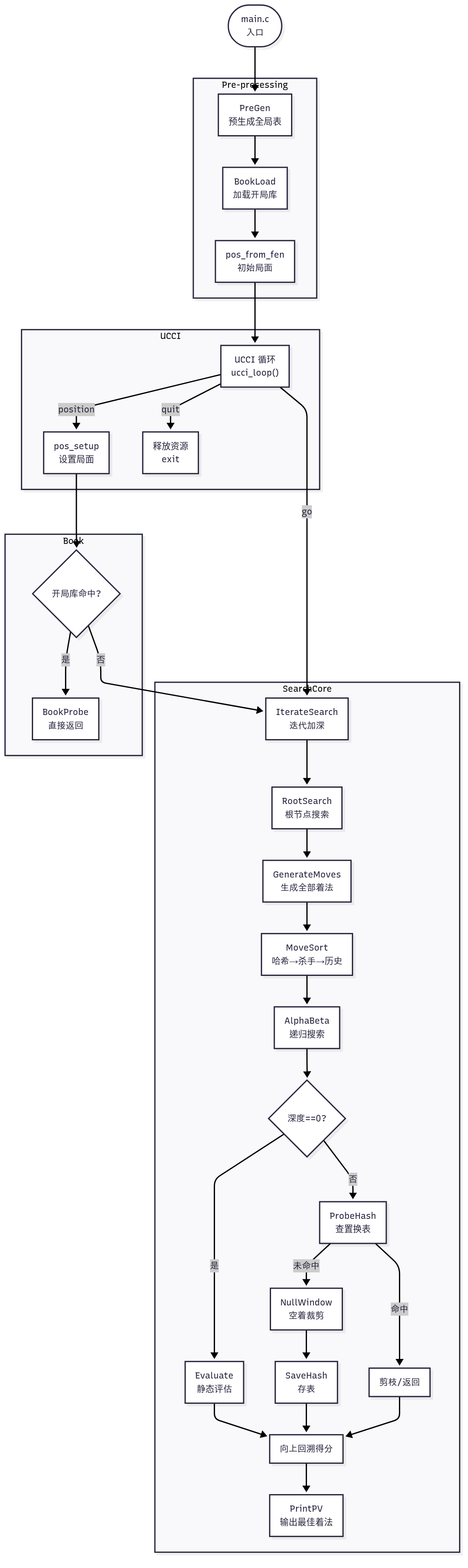
中国象棋eleeye流程
你能获取https://github.com/xqbase/eleeye/tree/master/eleeye 项目并解释该项目吗? 我来帮您获取并解释这个 GitHub 项目。看起来页面内容被截断了
中国象棋估值策略
估算体系(Evaluation Systems)并不是单一的,而是多层、多阶段、多用途的。它们各司其职,不直接累加,而是通过逻辑顺序、条件判断、选择性启用的方式协同工作。 ✅ 一、估算体系总览 表格
给出中国象棋伪代码逻辑链
主评估入口:Evaluate(pos, vlAlpha, vlBeta) │ ├─ 1. 基础层:PreEval 已初始化 │ vlWhite = 红方棋子位置价值之和 │ vlBla
epr佯谬与定域性
epr佯谬 EPR佯谬的定义 EPR佯谬,全称爱因斯坦-波多尔斯基-罗森佯谬,是由爱因斯坦、波多尔斯基和罗森在1935年提出的一个思想实验。这个佯谬的核心在于质疑量子力学的完备性,特别是关于量子纠缠现
固有时
固有时 “固有时”(proper time)是相对论中一个核心概念,指在某一参考系中,同一地点发生的两个事件之间的时间间隔,即由随事件一起运动的时钟所测得的时间。它是不依赖于观测者参考系的时间量,因此
更换docker国内镜像源
✅ 步骤一:编辑配置文件 CentOS 7 的 Docker 配置文件路径是: bash 复制 /etc/docker/daemon.json 如果文件不存在,可以新建一个。 bash 复制 sudo
git 如何查看当前项目最后一次提交的哈希值
你可以使用下面的命令来查看当前 Git 项目最后一次提交的哈希值(完整 40 位): bash 复制 git rev-parse HEAD 如果你只想看前 7 位短哈希(很多平台默认显示的格式),可以
用python写一个程序判断输入的数是不是质数(关于6)
下面是一个简单的Python程序,用于判断用户输入的数是否为质数: def is_prime(num): # 质数定义为大于1的自然数,且除了1和它本身外不再有其他因数 if num